13+ time derivative of a vector in a rotating coordinate system
Instead of forces Lagrangian mechanics uses the energies in the system. When students become active doers of mathematics the greatest gains of their mathematical thinking can be realized.

Pdf Irodov Problems In General Physics Lokesh Khandelwal Academia Edu
ASCII characters only characters found on a standard US keyboard.

. Even though the triangulation is 2D. The Calculator filter computes a new data array or new point coordinates as a function of existing scalar or vector arrays. If m is an objects mass and v is its velocity also a vector quantity then the objects momentum p is.
In the Cartesian coordinate system these are called x y. In mathematics the cross product or vector product occasionally directed area product to emphasize its geometric significance is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space named here and is denoted by the symbol Given two linearly independent vectors a and b the cross product a b read a cross b is a vector that is. Both members and non-members can engage with resources to support the implementation of the Notice and Wonder strategy on this webpage.
737 Landau and Lifshitz argue that the Lagrangian formulation makes the conceptual content of classical mechanics more clear than starting with Newtons laws. From the instantaneous position r rt instantaneous meaning at an instant value of time t the instantaneous velocity v vt and acceleration a at have the general coordinate-independent definitions. The dAlembert operator on Minkowski space is α α as in the vector formulation.
The extension inserts a minus sign automatically to correct for this. Any of the position vectors can be denoted r k where k 1 2 N labels the particles. Manifolds need not be connected all in one piece.
We would like to show you a description here but the site wont allow us. The latest Lifestyle Daily Life news tips opinion and advice from The Sydney Morning Herald covering life and relationships beauty fashion health wellbeing. The coefficients are a set of 16 real-valued functions since the tensor is a tensor field which is defined at all points of a spacetime manifold.
We start by taking the normalized vector for the derivative at some point on the curve. Browse our listings to find jobs in Germany for expats including jobs for English speakers or those in your native language. An example is a pair of separate circles.
This is the derivative of the momentum 4-vector with respect to. If the dot product of two vectors is defineda scalar-valued product of two vectorsthen it is also. Suppose the frames are aligned at and the -axis is the axis of rotationThen for a counterclockwise rotation through angle.
We normalize it so the maths is less work. The left-hand side is the time derivative of the momentum and the right-hand side is the force represented in terms of the potential energy. The time-derivatives of these unit vectors are found next.
Since photons travel at the speed of light their world lines have a slope of 1. In the International System of Units SI the unit of measurement of. 6 to 30 characters long.
How quickly an object rotates or revolves relative to a point or axis. In general spacetimes the coordinate system x α is arbitrary the covariant derivative α the Ricci tensor R αβ and raising and lowering of indices are defined by the Lorentzian metric g αβ and the dAlembert operator is defined as α. The vertical time coordinate is scaled by so that it has the same units meters as the horizontal space coordinate.
A holonomic constraint is a constraint equation of the form for particle k which connects all the 3 spatial coordinates of that. Where t x y z and t x y z are the coordinates of an event in two frames with the origins coinciding at t t 0 where the primed frame is seen from the unprimed frame as moving with speed v along the x-axis where c is the speed of light and is the Lorentz factorWhen speed v is much smaller than c the Lorentz factor is negligibly different from 1 but as v. Manifolds need not be closed.
Thus a line segment without its end points is a manifoldThey are never countable unless the dimension of the manifold is 0Putting these freedoms together other examples of manifolds are a parabola a hyperbola and the locus of points on a cubic curve y 2. You can either have the routine calculate the first derivative of the function numerically or supply the first derivative yourself. In mathematics the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.
The factors are one-form gradients of the scalar coordinate fields The metric is thus a linear combination of tensor products of one-form gradients of coordinates. Notice that velocity always points in the direction of motion in other words for a curved path it is the tangent vectorLoosely speaking first order derivatives are related to. In order for the metric to be symmetric we must have.
The magnitude of the pseudovector represents the angular speed the rate at which the object. This result can be obtained from a rotation matrix. Euclidean and affine vectors.
For an N particle system in 3 dimensions there are 3N second order ordinary differential equations in the positions of the particles to solve for. And then were done we found the normal vector. Must contain at least 4 different symbols.
If point-centered arrays are used in the computation of a new data array the resulting array will also be point-centered. The reference point analogous to the origin of a Cartesian coordinate system is called the pole and the ray from the pole in the reference direction is the polar axis. Applies to each particle.
Rotating coordinates is actually very easy if you know the rule for it. Introduce the unit vectors ȷ representing standard unit basis vectors in the rotating frame. In addition the notion of direction is strictly associated with the notion of an angle between two vectors.
The above-mentioned triad of unit vectors is also called a basisSpecifying the coordinates components of vectors of this basis in its current rotated position in terms of the reference non-rotated coordinate axes will completely describe the rotationThe three unit vectors and that form the rotated basis each consist of 3 coordinates yielding a total of 9 parameters. A Fourier transform FT is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial frequency or temporal frequencyThat process is also called analysisAn example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitchesThe term Fourier transform refers to. In Newtonian mechanics linear momentum translational momentum or simply momentum is the product of the mass and velocity of an object.
The function is plotted in the SVG coordinate system which has the y-axis upside down. For a system of N particles in 3D real coordinate space the position vector of each particle can be written as a 3-tuple in Cartesian coordinates. It is a vector quantity possessing a magnitude and a direction.
We can use the cross product a second time and immediately get our normal vector. In the geometrical and physical settings it is sometimes possible to associate in a natural way a length or magnitude and a direction to vectors. In physics angular velocity or rotational velocity ω or Ω also known as angular frequency vector is a pseudovector representation of how fast the angular position or orientation of an object changes with time ie.
The central quantity of Lagrangian mechanics is the Lagrangian a function which summarizes the dynamics of the. Thus the triangulation is constructed in the x-y plane.

Lec 04 Total Derivative Of A Vector In A Rotating Frame Of Reference Youtube

Time Derivatives In A Rotating Frame Of Reference Youtube

Lec 04 Total Derivative Of A Vector In A Rotating Frame Of Reference Youtube
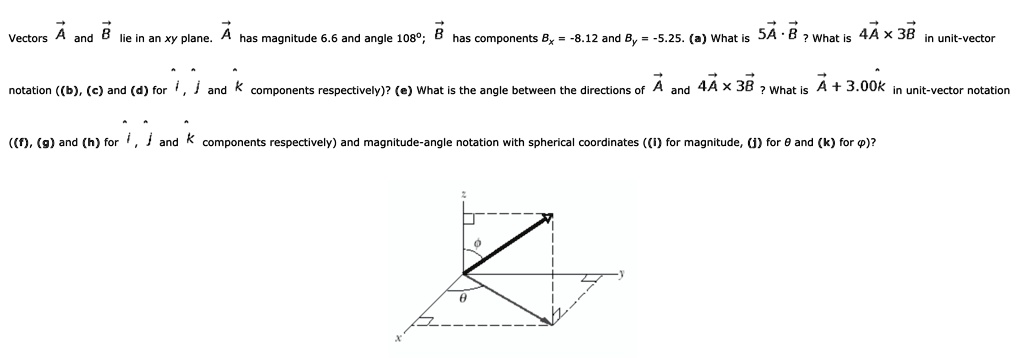
Browse Questions For Physics 101 Mechanics
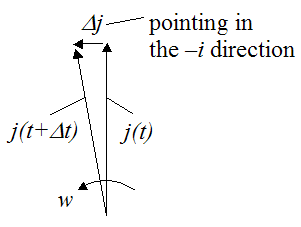
Vector Derivative
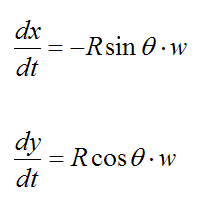
Vector Derivative

Rotation Matrix Time Derivative Youtube

Time Derivatives Of Unit Vectors For Polar Coordinates Full Derivation 2d Coordinate Systems Youtube
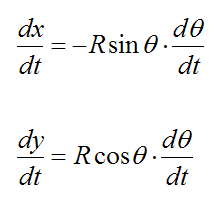
Vector Derivative

Spring Course Listing Uss At Tufts Tufts University

Newtonian Mechanics The Time Derivatives Of Vectors In Rotating Frames Physics Stack Exchange

Time Derivatives In A Rotating Frame Of Reference Youtube

Lrs Bianchi Type V Perfect Fluid Cosmological Model In F R T Theory

Physics Derivative Of Rotating Unit Vector In Coordinate Free Maner Mathematics Stack Exchange
The Expected Value Explanation Examples

Total Differentiation Of A Vector In A Rotating System Youtube

Coordinate Systems Relation Between Time Derivatives Observed From Fixed And Rotating Frames Physics Stack Exchange